To explore graphical and numerical summaries of continuous data, let’s consider
a dataset which contains daily air quality measurements in New York from May to
September 1973. Let’s look at the first 10 rows of the data:
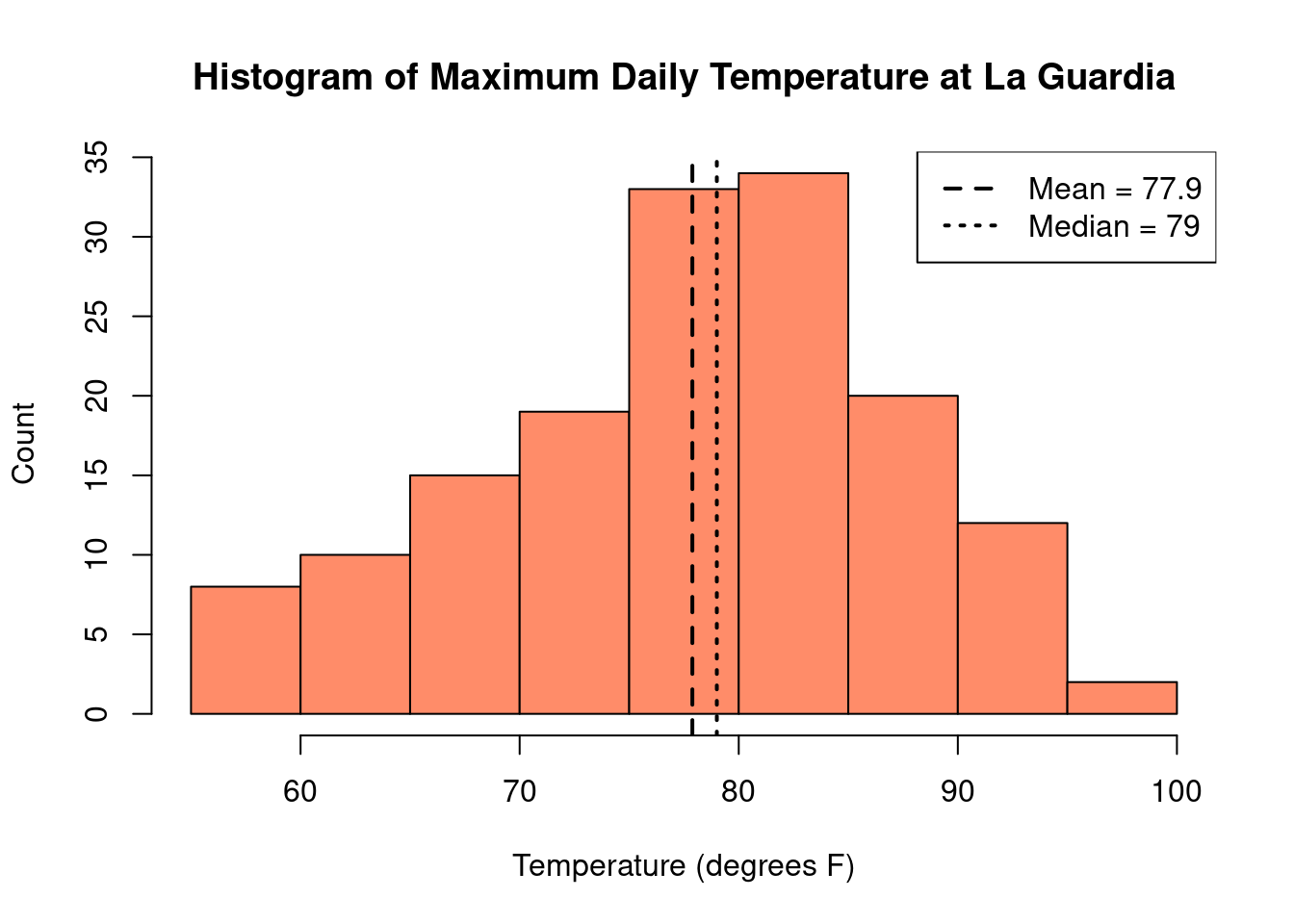
In the histogram of temperature, we can readily see that on most days between May and
September, the maximum temperature at La Guardia was between 75°F - 85°F. Some
days were particularly chilly, with temperatures below 60°F and some days
were quite hot, with temperatures above 90°F.
Measures of Centrality
While nothing can replace a picture, sometimes it is preferable to summarize our data with one or two numbers characterizing the most important information about the distribution. Often, we are most interested in information that describes the ‘center’ of a distribution, where the bulk of our data tends to aggregate. The two most common ways to describe the center are with the mean and the median.
The mean is the most commonly used measure of the center of a distribution.
Simply enough, the mean is found by taking the sum of all of the observations,
and dividing by the total. With \(n\) observations, \(x_1, x_2, ..., x_n\),
we can mathematically express the mean, denoted as \(\bar{x}\) (x-bar), in the following way:
\[
\bar{x} = \frac{x_1 + x_2 + \dots + x_n}{n} = \frac1n \sum_{i=1}^n x_i
\]
The median is another common measure of the center of a distribution. In
particular, for a set of observations, the median is an observed value that is
both larger than half of the observations, as well as smaller than half of the
observations. In other words, if we were to line our data up from smallest to largest, the median value would be right in the middle. Indeed, to find the median, we begin by
arranging our data from smallest to largest. If the total number of observations,
\(n\), is odd, then the median is simply the middle observation; if \(n\) is even,
it is the average of the middle two.
Examples:
- \(1, 2, 2, 3, {\color{red} 5}, 7, 9, 10, 11 \quad \Rightarrow \quad \text{Median} = 5\)
- \(1,2,2,3, {\color{red} 5}, {\color{red} 6}, 7, 9, 10, 11, \quad \Rightarrow \quad \text{Median} = \frac{(5+6)}{2} = 5.5\)
For the New York temperature data, the mean is 77.9°F and
the median is 79°F. These values are very similar to
each other, and both fall near the peak in the histogram.
However, it is not always the case that the mean and median will be similar. Let’s
consider an example in Table 2.4 where we collect \(n = 10\) samples of salaries for University
of Iowa employees:
Table 2.4: University of Iowa Salaries
|
$31,176
|
$130,000
|
|
$50,879
|
$37,876
|
|
$34,619
|
$144,600
|
|
$103,000
|
$48,962
|
|
$36,549
|
$5,075,000
|
For our sample, we find that the mean is $569,266, but the median is
($48,962 + $50,879) / 2 = $49,921. It turns out our sample included the highest
paid university employee – the head football coach. This extremely high salary
has caused the mean to be very large – larger than the remaining 90% of the salaries in our
sample combined. The median, on the other hand, ignoring the extremes ends of our distribution and focusing on the middle, is not impacted by the football coach’s
salary. Consequently, in this case, it is a much better reflection of the typically university employee’s
salary than the estimate found with the mean.
This one high salary, which is not representative of most of the salaries
collected, is known as an outlier. From the example above, we have seen that
the mean is highly sensitive to the presence of outliers while the median is not.
Measures that are less sensitive to outliers are called robust measures. The median is a robust estimator of the center of the data.
We have seen an example where the mean and median are quite close and an example
where they are wildly different. This begs the broader question – when might we
expect these measures of central tendency to be the same, and when might we expect
them to differ? Here, we consider a collection of histograms showing us different “shapes” that the distributions of our data may take.
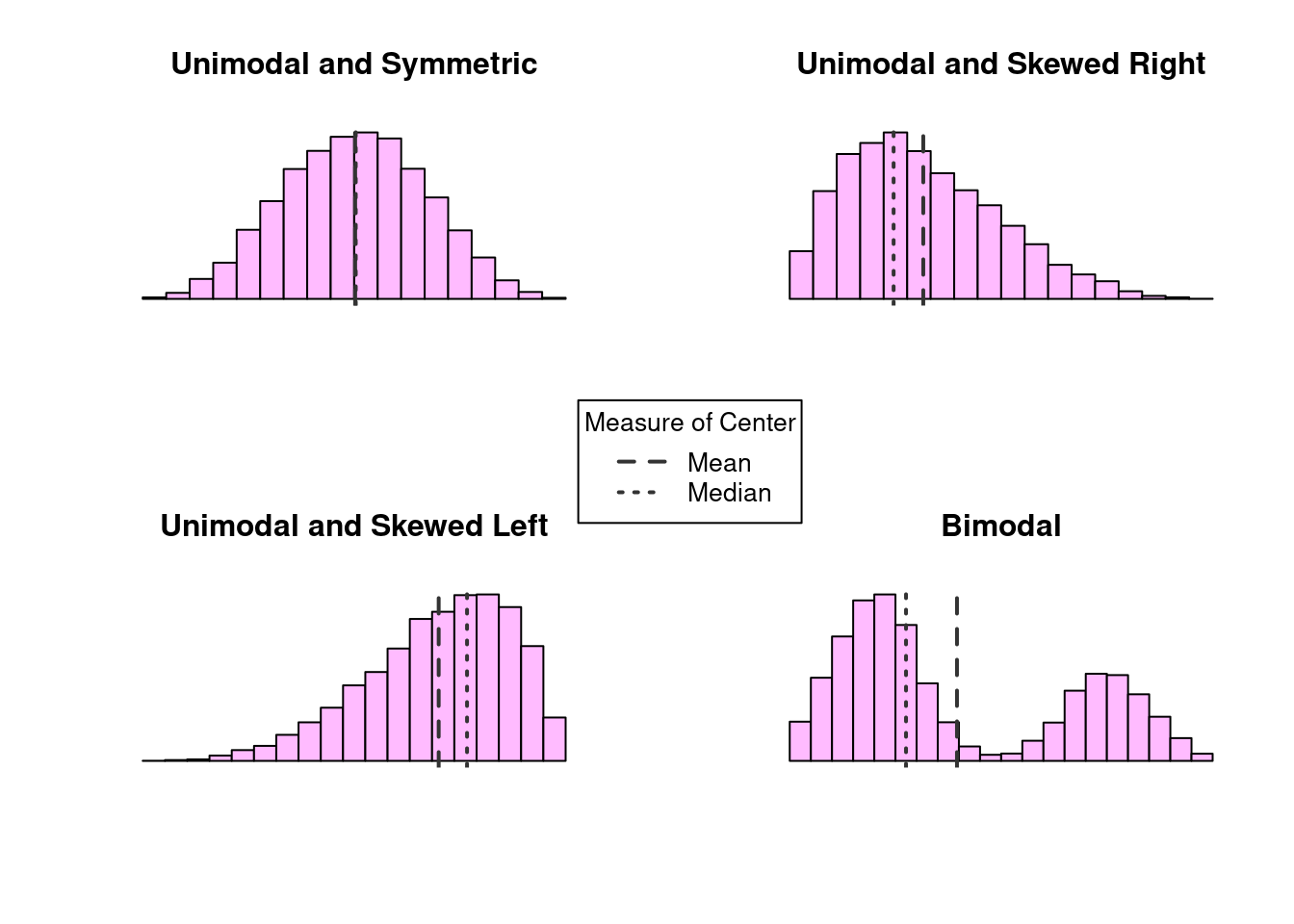
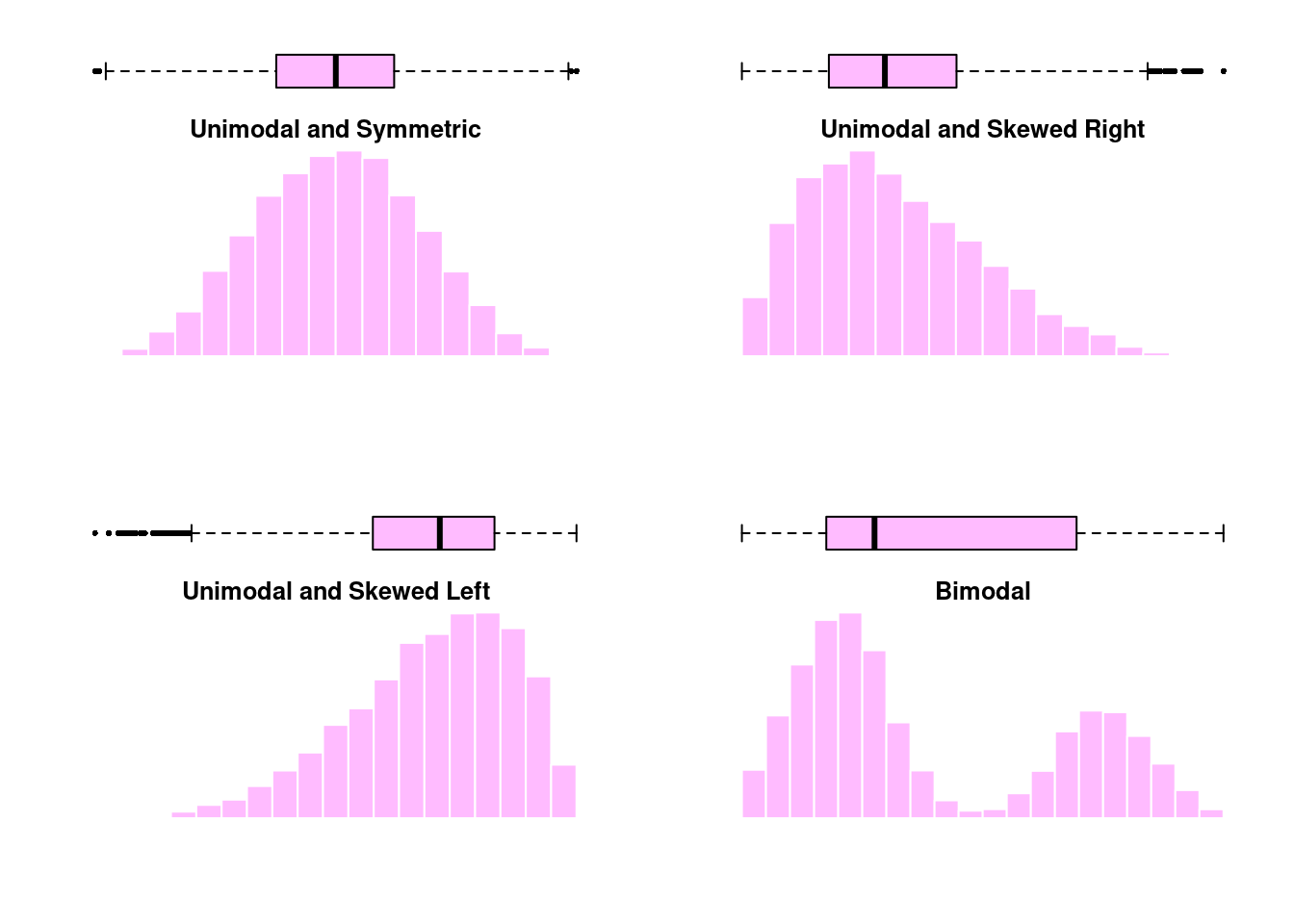
The shape of a distribution is often characterized by its modality and its skew. The modality of a distribution is a statement about its modes, or “peaks”. Distributions with a single peak are called unimodal, whereas distributions with two peaks are call bimodal. Multimodal distributions are those with three or more peaks. The skew on the other hand describes how our data relates to those peaks. Distributions in which the data is dispersed evenly on either side of a peak are called symmetric distributions; otherwise, the distribution is considered skewed. The direction of the skew is towards the side in which the tail is longest. Examples of modality and skew are presented in Figure 2.1.
When the data is unimodal and symmetric, the mean and median are indistinguishable.
However, when there is skew or multiple peaks, we see the mean and median start
to differ. When the distribution is skewed, the mean is pulled towards the tail.
On the other hand, the number of very large/small observations is relatively small,
so the median remains closer to the peak where the majority of data lies. When
the distribution is bimodal, neither the mean or median can summarize the distribution
well. In that case, it might be better to characterize the center of each peak individually.
Mean: The average value, denoted \(\bar{x}\) and computed as the sum of the observations divided by the number of obervations
Median: The middle value or 50th percentile, the value such that half the observations lie below it and half above
Outlier: Extreme observations that fall far away from the rest of the data
Robust: Measures that are not sensitive to outliers
Unimodal: Characterization of a distribution with one peak
Bimodal: Characterization of a distribution with two peaks
Multimodal: Characterization of a distribution with three or more peaks
Symmetric: Characterization of a distribution with equal tails on both sides of the peak
Skewed right: Characterization of a distribution with a large tail to the right of the peak
Skewed left: Characterization of a distribution with a large tail to the left of the peak
Measures of Dispersion
In addition to measuring the center of the distribution, we are also interested
in the spread or dispersion of the data. Two distributions could have the
same mean or median without necessarily having the same shape.
For example, consider the two distributions of data shown below. Each distribution
represents a sample of 1,000 observations with mean of 100.
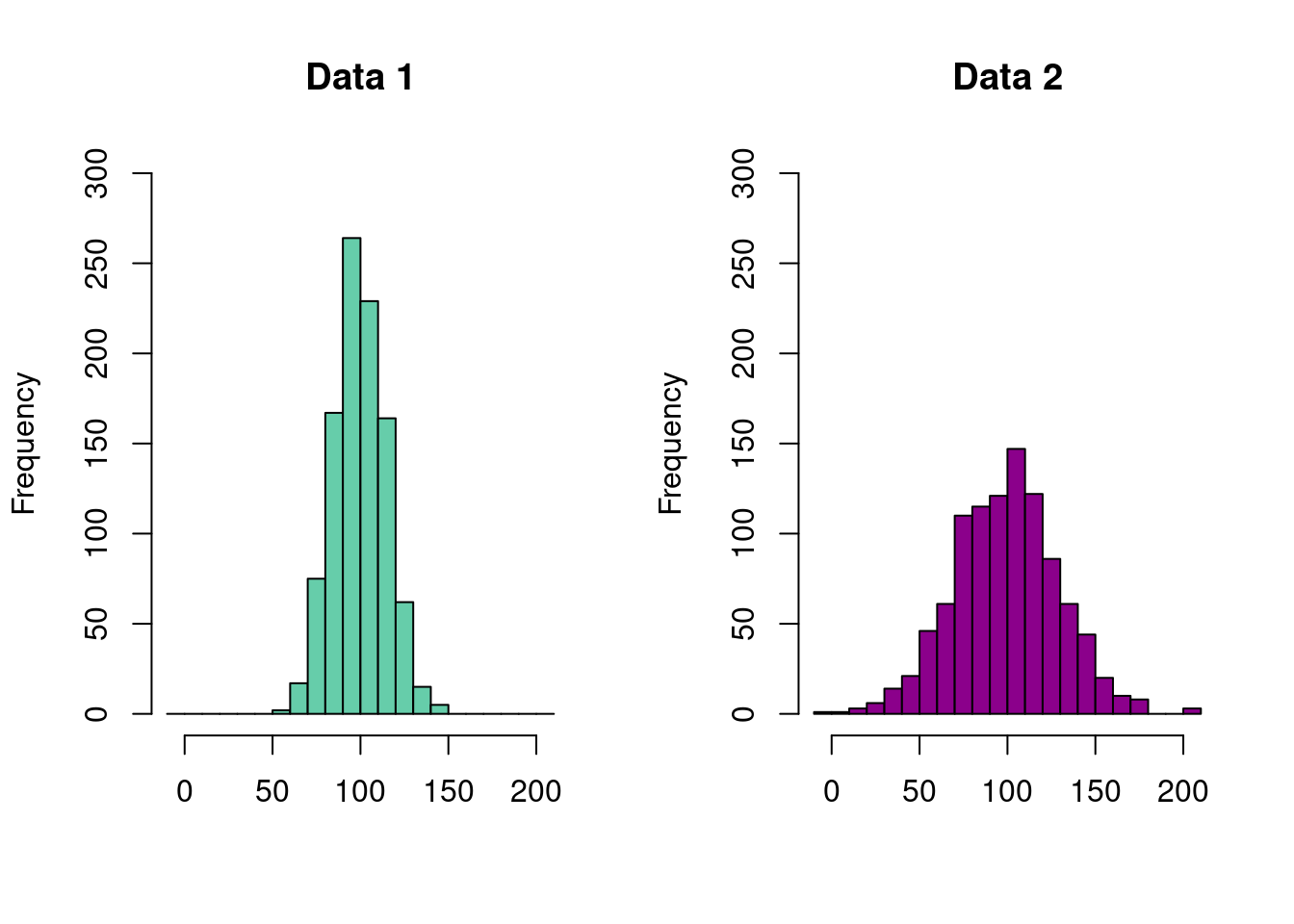
Despite the mean values of each of these distributions being the same, we can clearly see that they are different. On the left, we see that nearly the entire range of the observed data falls between 50 and 150. For the distribution on the right, the data is much more spread out, taking on values near 0 and 200. In order to accurately capture these differences, we need a second numerical summary describing the degree to which the data is spread about its center. Here, we consider two broad categories – those based on percentiles and those based on the variance.
Percentiles and IQR
Perhaps the most intuitive methods of describing the dispersion of our data are those associated with percentile-based summaries. Formally, the \(p\)th percentile is some value \(V_p\) such that
- \(p\%\) of observations are less than or equal to \(V_p\)
- \((100 - p)\%\) of observations are greater than or equal to \(V_p\)
Informally, percentiles quantify where observations fall, relative to all of the other observations in the data. Two of the best known percentiles are the \(1^{st}\) and \(99^{th}\) percentiles, more commonly referred to as the minimum and maximum values. Together, these two numbers describe the range of our data. The next most common value is the \(50^{th}\) percentile – the median – which we recall describes the value for which half of our observations and greater (or lesser) than. We are also often interested in determining the \(25^{th}\) and \(75^{th}\) as well, which, respectively, mark the midpoints between the minimum and the median and the median and the maximum. Along with the median, these three percentiles make up the quartiles of our data, denoted
\[
\begin{align*}
Q_1 &= 25^{th} \text{ percentile} = 1^{st} \text{ or lower quartile} \\
Q_2 &= 50^{th} \text{ percentile} = 2^{nd} \text{quartile or median} \\
Q_3 &= 75^{th} \text{ percentile} = 3^{rd} \text{ or upper quartile}
\end{align*}
\]
We know the median, \(M\), is the value such that 50% of observations are less than
the median and 50% are greater than it. \(Q_1\) can be said to represent the median of the
smaller 50% of all observations, while \(Q_3\) can be said to be the median of
larger 50%. In other words, 25% of the data is below \(Q_1\), 25% of the data is
between \(Q_1\) and \(M\), 25% of the data is between \(M\) and \(Q_3\), and the
remaining 25% of the data is larger than \(Q_3\).
A commonly used percentile-based measure of spread combining these measures is the interquartile range (IQR), defined as
\[\text{IRQ} = Q_3 - Q_1.\]
Because it is the difference between the upper and lower quartile, it represents
the distance covering the middle 50% of the data. We may also report the range
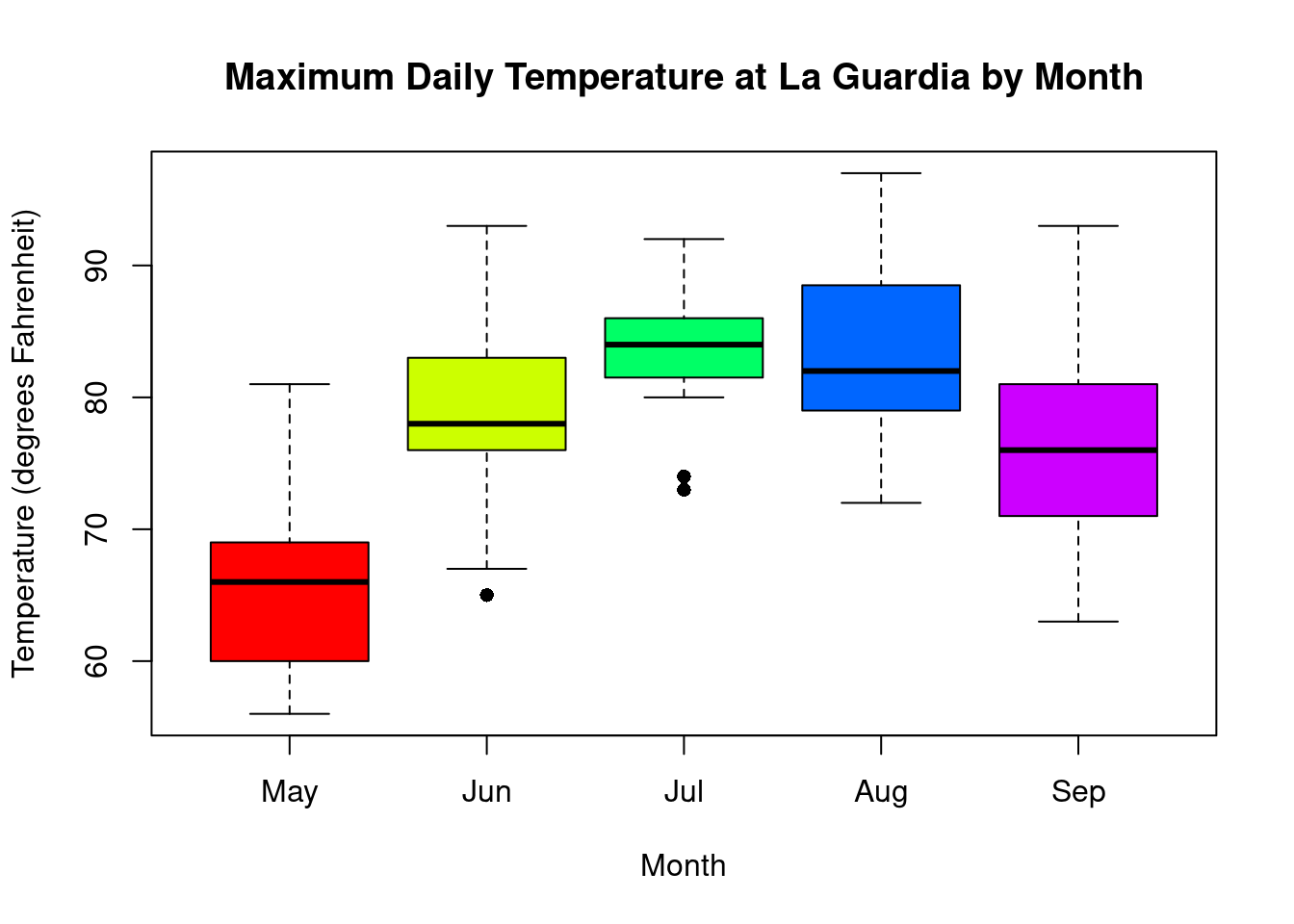
as an interval as \((Q_1, Q_3)\). For the New York temperature data, \(Q_1 = 72\), \(Q_3 = 85\). The IQR is therefore \(85 - 72 = 13\) and tells us that 50% of the days
between May and September had temperatures between 72°F and 85°F.
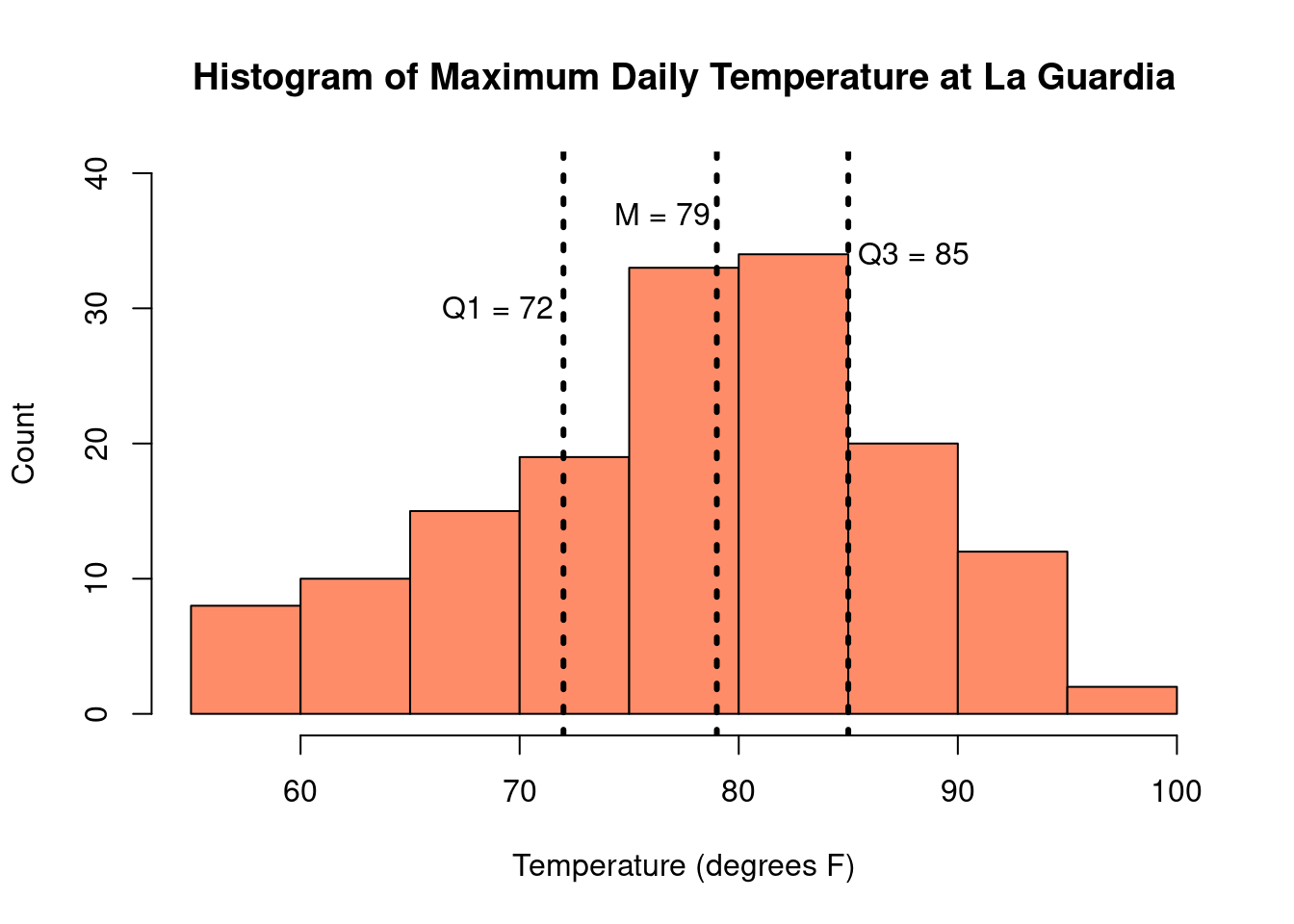
The IQR is not impacted by the presence of outliers, so it is considered a robust
measure of the spread of the data. So, like the median, it enjoys the quality of being a robust measure of the data.
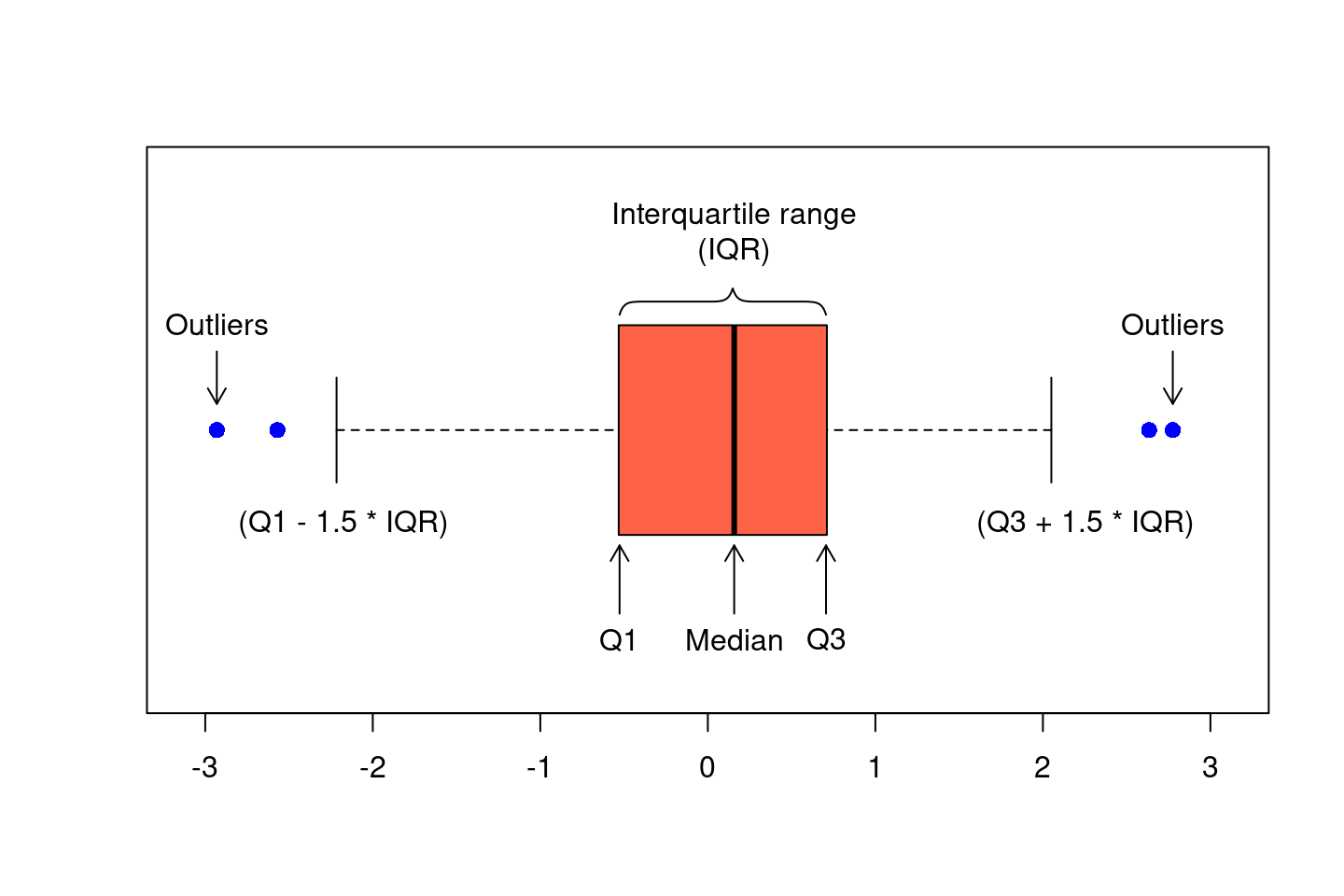
Percentiles are also used to create another common visual representation of
continuous data: the boxplot, also known as a box-and-whisker plot. A
boxplot consist of the following elements:
- A box, indicating the Interquartile Range (IQR), bounded by the values \(Q_1\) and \(Q_3\)
- The median, or \(Q_2\), represented by the line drawn within the box
- The “whiskers”, extending out of the box, which can be defined in a number of
ways. Commonly, the whiskers are 1.5 times the length of the IQR from either
\(Q_1\) or \(Q_3\)
- Outliers, presented as small circles or dots, and are values in the data that are not present within the bounds set by either the box or whiskers
Just like histograms, boxplots can also illustrate the skew of a data. In a
histogram, the skewed was named after the location of the tail and in a boxplot,
this corresponds to the side with a longer whisker. Here we can see histograms
and boxplots for various distributions of data.
Percentile: A value, \(V_p\) such that \(p\)% of observations are smaller than \(V_p\) and \(1-p\)% of observations are larger than \(V_p\)
Range: The distance between the minimum and maximum values in a dataset
Interquartile range (IQR): The middle 50% of the data, the difference between the upper and lower quartiles
Boxplot/box-and-whisker plot: Visualization of continuous data which is based on percentiles
Variance and Standard Deviation
The variance and the standard deviation are numerical summaries which
quantify how spread out the distribution is around its mean. This is done by
calculating how far away each observation is from the mean, squaring that difference,
and then taking an average over all observations. For a sample of \(n\) observations
\(x_1, x_2, ..., x_n\), the variance, denoted by \(s^2\), is calculated as:
\[
s^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2.
\]
The standard deviation, denoted \(s\), is a function of the variance.
Specifically, it is the square root of the variance \(s = \sqrt{s^2}\). Because the
variance uses the squared differences between each observation and the mean, its
units are the square of the units of the original data. For example, the
New York temperature measurements have a mean of 77.9°F and a variance
of 89.6°F2, a value that does not readily lend itself to interpretation. The standard deviation, on the other hand, takes the square root, putting
the units back on the original scale. For the temperature data, the standard
deviation is 9.5°F. Because of this, the standard deviation is often
preferred as a measure of spread over the variance.
Finally, unlike the median and the IQR, which are based the percentiles of the observed data, both the variance and standard deviation are calculated based on the mean. Recall that the mean is not a robust outlier and is highly sensitive to skew or the presence of outliers. Consequently, the variance and the standard deviation are also very sensitive. When the data are unimodal and symmetric, choosing between the mean/standard deviation and the median/IQR is largely a matter of preference. However, when the data is skewed or has large outliers, more robust statistics such as the median and IQR are preferred.
The applet below is designed to help illustrate the properties of the mean and
standard deviation. You can vary the mean between -10 and 10 and the standard
deviation between 1 and 20. The histogram on the right displays the unimodal and
symmetric distribution of data with the specified mean and standard deviation.
-
Set the standard deviation to 8 and use the slider to vary the mean of the
distribution. What properties of the histogram change as the mean is varied?
What stays the same?
-
Now, set the mean to 0 and vary the standard deviation. What properties of
the histogram change as the standard deviation is varied? What stays the same?
-
Let’s examine more closely how the standard deviation affects the distribution
of data. Keep the mean at 0, and set the standard deviation to 4, 8, 12, 16,
and 20.
-
For each standard deviation, fill out the following table with the
approximate minimum and maximum values of the data.
| Standard deviation |
Minimum and maximum |
| 4 |
|
| 8 |
|
| 12 |
|
| 16 |
|
| 20 |
|
-
What do you notice about the relationship between the standard deviation
and the minimum/maximum values observed in the data? Is there any noticeable
pattern in your table?
Variance: The average of the squared differences between each data value and the mean, denoted \(s^2\)
Standard deviation: The square root of the variance, denoted \(s\)
Percentile: Summaries providing the location of observations relative to all other observations in the data