1 Introduction

“So never lose an opportunity of urging a practical beginning, however small, for it is wonderful how often in such matters the mustard-seed germinates and roots itself.”

— Florence Nightingale

Learning objectives

Describe the field of statistics and its importance in scientific inquiry
Learn the scientific method, its purpose, and its connection to statistics
Understand the concepts in the general statistical framework

1.1 Statistics and Evidence-based Research

There are many definitions of statistics:

the science of learning from experiences
the study of collecting, analyzing, and interpreting data
the mathematics of uncertainty
a required college course designed to make everyone miserable

All of these definitions hold a degree truth (some more than others – we’ll let you guess which 😉). Statistics is a highly versatile field, with methods applicable to and used by a wide variety of disciplines. The importance of the field of statistics lies in it’s ability to quantify our uncertainty about a potential outcome – such as the most likely cause and treatment for a headache. Almost everything in life is associated with some uncertainty – the weather, your career, the connection between your genetics and your response to certain medications; however, just because something isn’t known with 100% certainty doesn’t mean we can’t understand it better. Statistics helps us understand the world better by allowing us to quantify our uncertainty, describe associations between phenomena, and make informed decisions.

And how exactly do researchers use statistics to quantify their uncertainty? Well, this is achieved by collecting data, or evidence, about whatever process is of interest. For example, if you want to know how likely it is to rain tomorrow, you might look at the weather in your location the past few days. Since rain can travel, you might also look at the recent weather in the surrounding areas. You could also evaluate historical weather records to determine if this season is known for being particularly rainy or dry in the past. These are all various examples of data you can collect to inform your weather prediction. In scientific research, data is obtained and investigated through statistical inquiry to help answer important questions:

Which drug should a doctor prescribe to treat an illness?
Can we predict the longevity of the national population to inform government decisions regarding Social Security?
What factors increase the risk of an individual developing coronary heart disease?

These questions are too important to be left to opinion, superstition, or conjecture. Consequently, there has been a tremendous push for objective, evidence-based decision making in medicine, public health, and policy making. Statistics and biostatistics are the sciences that allows us to make these difficult decisions. When studying humans, we can’t control every aspect of their life, such as what they eat or where they work. There are ethical considerations - if we wanted to research the effects of smoking on lung cancer, we would not be able to force people to smoke (or not). Humans are also incredibly diverse and variable, not to mention expensive to perform research upon. Despite these issues, there is a moral imperative to make decisions on potentially life-saving therapies as fast as possible. To make evidence-based conclusions, we need to collect, process, analyze, and interpret data in order to draw conclusions in an objective manner.

Definition 1.1

Evidence-based practice: Using sound research findings based on observed or collected data to make decisions

1.2 Scientific Method

In principle, people collect and process information every day of their lives. Since it’s something we do frequently, you might think we would be really good at it…but we’re not. Unfortunately, humans are not natural statisticians. We are not good at picking out patterns from a sea of noisy data. And, on the flip side, we are too good at picking out non-existent patterns from small numbers of observations. We also find it difficult to sort out the effects of multiple factors occurring simultaneously and we are subject to all sorts of biases depending on our personalities, emotions, and past experiences.

In order to mitigate any of our own personal biases when answering important questions about the way the world works (i.e., to do good science), we must be careful to be rigorous in the way we proceed. The scientific method is the process used to answer scientific questions.

Ask a question
Construct a hypothesis
Test your hypothesis with a study or an experiment
Analyze data and draw conclusions
Communicate results

As an example of the scientific method, consider that you would like to start a garden, but you are not sure which type of fertilizer is best. If there are three types of fertilizer you cannot decided between, you might proceed through the scientific method as follows:

Ask a question

Of fertilizers A, B, and C, which will yield the fastest plant growth in my garden?

Construct a hypothesis

You may have read some reviews for each type of fertilizer online. Fertilizer A has 4.5 stars, fertilizer B as 4.2 stars, and fertilizer C has 4.6 stars. Thus, you may hypothesize that fertilizer C leads to the fastest plant growth, followed by fertilizer A, and that fertilizer B has the slowest plant growth.

Test your hypothesis with a study or an experiment

To test your hypothesis, you can section off three areas of your garden. In each area, you use one of the three fertilizers and plant the same number and type of plants. In order for your experiment to be fair, you will want to make sure each of the three areas is equal-size, gets the same amount of sunlight, is watered the same amount, etc.

Analyze data and draw conclusions

After 5 weeks, you measure the height of each plant which use each type of fertilizer. Taking the average plant height from each of the three sections of your garden, you find that when fertilizer A was used, the average plant height was the tallest and thus you conclude that fertilizer A is the best for your garden.

Communicate results

Other gardeners in your area may be interested in your results. You may share with them your recommendation for fertilizer A, which is backed by a well-controlled experiment.

Even in this relatively simple example, you can see how much care is required to have a valid experiment. There are many other factors that may also influence your decision on the best fertilizer, such as the price and availability. It’s also possible that fertilizer A ended up with the fastest average plant growth just due to random chance, and if you repeated the entire experiment again you might find fertilizer B or C to result in taller plants.

Definition 1.2

Scientific method: Five steps that can be used to acquire knowledge without incorporating personal opinion

1.3 Statistical framework

As we saw in the fertilizer example, collecting and analyzing data can be complicated. Statistics helps us design studies, test hypotheses, and use data to make scientifically valid conclusions about the world. In general, scientists use the scientific method to make generalizations about classes of people on the basis of their studies. The class of people that they are trying to make generalizations about is called the population. Most of the time, it is impractical and expensive to study all individuals in a population - although many governments do the best they can every 10 years. Instead of sampling everyone in the population, or taking a census, typically we study only a portion of the population called the sample. In order to determine how best to obtain a sample to answer the research questions, we must be cautious about the study design. Then, researchers make generalizations, or inference, about the entire population based on studying the sample. We can visualize the statistical framework using this diagram:

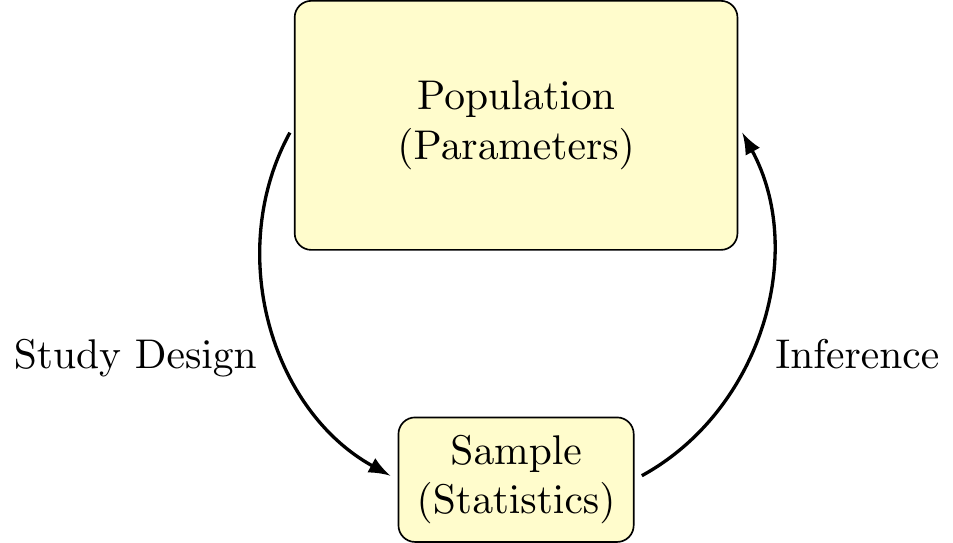
Figure 1.1: Statistical Framework

Throughout this book, we will dive deeper in to each aspect of the statistical framework. We consider two broad categories of statistical analysis: descriptive statistics, which deals with methods for summarizing and/or presenting data and inferential statistics.

Definition 1.3

Population: The group towards which scientists attempt to generalize

Census: A study which includes all members of the population

Sample: A portion of the population which is part of the study

Study design: The process of obtaining the best sample to answer the research questions

Inference: The process of making generalizations about the population

Descriptive statistics: Methods for summarizing and/or presenting data

Inferential statistics: Methods for making generalizations about a population using information contained in the sample